Topo Sampler: A Topology Constrained Noise Sampling for GANs

Abstract

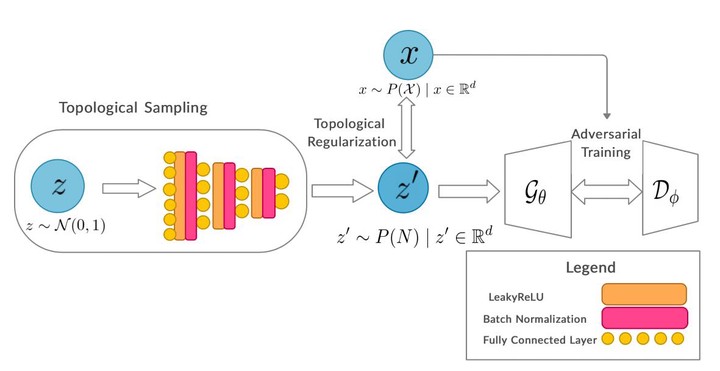
This work studies disconnected manifold learning in generative models in the light of point-set topology and persistent homology. Under this formalism, the topological similarity of latent space in generative models with the underlying manifold of data distribution facilitates better generalization. To achieve this, we introduce a topology-constrained noise sampler, responsible for mapping the samples from Gaussian spheres to a latent embedding space, which in turn is constrained to be topologically similar to the manifold underlying the data distribution. We study the effectiveness of this method in GANs for learning disconnected manifolds. This is ongoing research, with the current report containing preliminary empirical experiments.

Sayantan Das

Independent Researcher

My research interests include differential geometry,topological data analysis and tractable probabilistic inference.